
Alles, was sich Sprache nennt, ist ein Alphabet aus symbolischen Zeichen, deren Verwendung die Teilnahme der Sprechenden an einer Vergangenheit voraussetzt; wie aber soll man anderen das unendliche Aleph mitteilen, wenn es meine schaudernde Erinnerung kaum zu fassen vermag?
Jorge Luis Borges: Das Aleph
Bis jetzt haben wir nur gezählt; jetzt wollen wir auch messen oder wiegen. Dazu fassen wir Elemente zu einer Menge zusammen, was wir durch die geschweiften (oder einfacher durch die runden) Klammern andeuten: M = (a, b, c …)
Wir wollen wissen: Wie groß ist diese Menge? Wieviel „wiegt“ sie? Die Größe einer Menge bezeichnet man auch als ihre Mächtigkeit und kennzeichnet sie durch zwei Striche:
IMI = Mächtigkeit der Menge M
IMI ist eine Zahl, aber weil sie diesmal keine Ordnung, keine Reihenfolge bezeichnet, sondern eben eine „Mächtigkeit“, wird sie Kardinalzahl genannt. Sie wissen ja: Ein Kardinal ist etwas Mächtiges, jedenfalls in der katholischen Kirche, nicht unter den Schmetterlingen oder Vögeln.
Wie bestimmt man die Mächtigkeit einer Menge? Im Endlichen ist die Sache einfach. Schauen wir uns diese Mengen an:
M1 = (1,2,3,4,5)
M2 = (0,1,2,3,4)
M3 = (4,1,3,5,2)
M4 = (Abraham, Berta, Cäsar, Doris, Ernst)
M5 = (ω,ω+1,ω+2,ω+3,ε0)
Wie groß sind sie? Offenbar alle gleich; sie haben die Mächtigkeit „5“. Und wie haben wir das herausbekommen? Indem wir jede Menge den natürlichen Zahlen (in natürlicher Reihenfolge) zuordnen. Wir bilden also Paare zwischen den Elementen der Menge (dessen Größe bestimmt werden soll) und den natürlichen Zahlen, beginnend mit „1“.
Bei M1 ist es klar. M2 wird schon schwieriger: Die Zahlen sind in natürlicher Reihenfolge, beginnen aber bei 0. Also aufgepasst: Die letzte Zahl zeigt in diesem Fall nicht die Mächtigkeit der Menge! M3 ist das Gleiche wie M1, aber die Elemente sind vertauscht. Was uns einen wichtigen Hinweis auf Kardinalzahlen gibt:
Bei Mengen kommt es auf die Reihenfolge der Elemente nicht an.
M4 besteht aus Namen, die man den natürlichen Zahlen zuordnen kann. Denn auf die Art der Elemente kommt es erst recht nicht an: Jedes Element hat das gleiche Gewicht, nämlich 1, unabhängig davon, was es sonst bedeutet. Diese Erkenntnis hilft uns beim Verständnis von M5, denn sie besteht aus lauter unendlichen Zahlen. Heißt das nicht, dass auch ihre Mächtigkeit unendlich ist? Keineswegs, denn eine Zahl wie ω ist nicht etwa unendlich groß, sie ist nur unendlich weit von uns entfernt. Doch als individuelle Zahl hat sie das gleiche Gewicht wie 1 oder 17 oder irgendeine andere, durch Zählen erzeugte Zahl.
Die Paarbildung als Mittel des Zählens funktioniert sogar dann, wenn wir gar nicht zählen können. Stellen wir uns vor, zwei Massai-Männer wollen herausfinden, wer die größere Herde besitzt. (Rinderherden erhöhen den Status bei den Massai.) Jede Herde enthält Dutzende von Rindern – so weit kann niemand zählen. Dennoch ist es ganz leicht heraus zu finden, wer von den beiden die größere Herde besitzt. Die Herden werden eingesperrt und einzeln durch ein Gatter gelassen, jeweils ein Rind von der einen und ein Rind von der anderen Herde. Wenn am Ende kein Rind übrig bleibt, dann sind die Herden gleich groß; ansonsten ist eine größer als die andere.
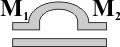
Wie man das Gewicht von Mengen (ihre Mächtigkeit) bestimmt: Man vergleicht sie mit einer bereits bekannten Menge. Je nachdem, ob die Waage im Gleichgewicht bleibt oder nach einer Seite ausschlägt, ist die zu wiegende Menge gleich, größer oder kleiner als die Vergleichsmenge.
Genauso machen es die Mathematiker. Sie vergleichen unbekannte Mengen mit bekannten, und das ist im Unendlichen die Menge aller natürlichen Zahlen, also die Mächtigkeit von N = (1,2,3,…)
Sie ist die wichtigste Vergleichsmenge im Unendlichen. Jetzt brauchen wir noch einen Namen für INI. Den hat sich ebenfalls Cantor ausgedacht, und in weiser Voraussicht fing er jetzt wieder von vorne an, mit dem ersten Buchstaben des hebräischen Alphabets: aleph (siehe Bild ganz rechts oben), genauer gesagt: aleph-0.
Aleph ist zwar der erste Buchstabe des phönizischen und des hebräischen Alphabets (und wurde später von den Griechen als „alpha“ übernommen), es ist aber kein Vokal, sondern ein Knacklaut. Im Hebräischen hat es den Zahlenwert 1 und ist Bestandteil von Adam (verwandt mit „adamah“ = Erde) und Abraham („Vater der Menge“). Auch in der Kabbala, der jüdischen mittelalterlichen Geheimlehre, spielt das aleph eine Rolle als Beginn einer Reise zu „En Soph“, dem durch kein Wissen erreichbaren Unendlichen, letztlich also zu Gott. Das En Soph ist wie ein Lichtstrahl von unendlicher Helligkeit, der sich der Unendlichkeit entgegen krümmt. Dort, wo das Licht auf den Raum trifft, zieht sich dieser zusammen und bildet die zehn Kreise des kabbalistischen Baums „Sephirot“. Da sich Cantor viel mit theologischen Spekulationen und jüdischer Mystik beschäftigte, waren ihm diese Zusammenhänge zweifellos bekannt.

Das „Gewicht“ (die Mächtigkeit) von N, der Menge der natürlichen Zahlen, beträgt aleph-0.
Rechnen mit aleph-0
Die Arithmetik unendlicher Kardinalzahlen ist wieder völlig anders als die unendlicher Ordinalzahlen. Bei den Ordinalzahlen stellten wir uns einfach vor, wie wir Stäbchen legen. Bei den Kardinalzahlen müssen wir immer in Mengen denken und dabei beachten, dass es auf die Reihenfolge von Stäbchen nicht ankommt. Also bedeutet ein Ausdruck wie aleph-0 + 1, dass wir zu der Menge aleph-0 ein Stäbchen hinzufügen. Auf der rechten Seite ist das nicht möglich, also müssen wir es links tun, und so entsteht die Menge
N‚ = (1,1,2,3,…)
und deren Mächtigkeit ist natürlich genauso aleph-0 wie die von N. Also gilt: aleph-0 + 1 = aleph-0. Da die Reihenfolge der Element bei Mengen egal ist, gilt natürlich auch 1 + aleph-0 = aleph-0
Das kommutative Gesetz ist hier erfüllt, aber mit „Stäbchen hinzufügen“ kommen wir nicht weiter. Wir können sogar unendlich viele Element hinzufügen, am „Gewicht“ der Menge ändert sich nichts, denn aleph-0 + aleph-0 entspricht der Menge (1,1,2,2,3,3,…), und deren Mächtigkeit ist genauso aleph-0. Weil aber aleph-0 + aleph-0 = 2 x aleph-0, bringt auch die Multiplikation uns nicht weiter. Sogar aleph-0 x aleph-0 = aleph-0, wie das Abzählen der rationalen Zahlen zeigt (siehe „Zwischenspiel: Wieviele Zahlen liegen zwischen 0 und 1?“). Wie kommen wir dann zu höheren Mächtigkeiten?