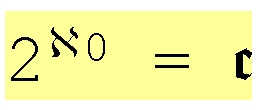
Mathematik ist die einzige Wissenschaft wo man nie weiß, worüber man redet, noch ob das, worüber man redet, wahr ist.
Bertrand Russell
Kommen wir über aleph-0 denn nie hinaus? Nun ja, wir haben noch nicht die Exponentiation. Aber was bedeutet beispielsweise 2^aleph-0 ? Um das zu begreifen, müssen wir wieder auf die Definition von Mengen zurückgreifen. Kombinatoriker wissen, dass der Ausdruck 2^n die Variation mit Wiederholung bedeutet, d.h. die Kombinationsmöglichkeiten von n Elementen zu beliebig großen Stücken der Länge 0 bis n. Schauen wir uns das an einem Beispiel an! Wir gehen aus von M = (1,2,3). Und hier sind alle möglichen Untermengen:
0 Elemente: O (die leere Menge) (1 Untermenge)
1 Element: (1),(2),(3) (3 Untermengen)
2 Elemente: (1,2),(1,3),(2,3) (3 Untermengen)
3 Elemente: (1,2,3) (1 Untermenge)
Summe: 1 + 3 + 3 + 1 = 8 Untermengen. Nun ist aber 8 = 2^3, also hier stimmt es. Allgemein kann man die Formel leicht beweisen. Es gibt sogar noch einen zweiten Beweis: „Alle Untermengen“ heißt in der Kombinatorik: alle möglichen Kombinationen zu 0 Elementen, zu 1 Element, zu 2 Elementen, usw. So kann man dafür auch die Formel für den Binomialkoeffizienten anwenden, aber das führt hier zu weit.
Mithin repräsentiert 2^aleph-0 die Menge aller Untermengen der natürlichen Zahlen. Eine solche Untermenge bezeichnet man auch als Potenzmenge, abgekürzt P(N) Aber wie groß ist diese Menge? Womöglich auch wieder nur abzählbar? Und was entspricht dieser Menge in der Realität?
Cantor fand heraus: Die Menge aller Untermenge entspricht den Zahlen (allen Zahlen, also den reellen Zahlen) auf der Zahlengeraden. Weil man dort jedes beliebige Intervall auf die ganze Zahlengerade abbilden kann, genügt es, das Intervall (0,1) zu betrachten. Wir müssen die Zahlen in diesem Intervall also so darstellen, dass man sie eindeutig den Untermengen von N zuweisen kann. Und das geht dadurch, dass wir nur zwei Ziffern verwenden, 0 und 1. Wir übersetzen also jede Zahl in das Dualsystem. Dann ist z.B.
0,1 = ½; 0,11 = ½ + ¼ = 0,75; usw.
Natürlich haben die meisten Zahlen unendlich viele Ziffern, genauso wie pi und fast alle anderen Zahlen. Wo wir nur endlich viele Ziffern hinschreiben müssen (wie bei den beiden Beispielen), da ergänzen wir den Rest durch Nullen.
Jetzt machen wir aus einer Zahl eine Menge. Die Regel: Wenn an der n-ten Stelle hinter dem Komma eine 1 erscheint, wähle die n-te Zahl aus der Menge der natürlichen Zahlen. Bei einer Null tue nichts. Beispiel:
Die Zahl 0,0 1 0 0 1 0 1 1 1 0 0 1 … entspricht der Untermenge
( 2 5 7 8 9 12 … Die Ziffern 1,3,4,6,10,11 entsprechen Nulen in der Zahlendarstellung, werden also nicht ausgewählt.
Durch die Zahl 0,0000… wird die Nullmenge ausgewählt, durch die Zahl 0,1111… die Menge N selbst. Auf diese Weise entspricht der Menge P(N) das Kontinuum der Zahlen, und weil man diesen Begriff im Lateinischen mit „C“ schreibt, wählte Cantor das kantige deutsche c (siehe Bild rechts oben) als Maß für das Kontinuum. Es gilt also:
2^aleph-0 = c (siehe Formel rechts oben)
Damit hätten wir die eine Frage beantwortet: P(N) ergibt alle Zahlen zwischen 0 und 1, nicht nur die Bruchzahlen.
Wirklich alle Zahlen? Der amerikanische Mathematiker Abraham Robinson (1918 – 1974) dachte sich unendlich viele Zahlen zwischen den reellen Zahlen aus, die er hyperreell nannte und die er in Beziehung setzte zu den „Differenzialen“ dx und dy aus der Differenzialrechnung. Dadurch vermehrt sich die Anzahl der Zahlen im Kontinuum, aber auch diese Zahlen kann man durch Dezimalbrüche mit 0en und Einsen darstellen. Und bei Conway haben wir die surrealen Zahlen kennen gelernt, die über diese Zahlen noch hinausgehen.
Jetzt zur zweiten Frage: Kann man diese Zahlen – also alle reellen Zahlen – abzählen oder nicht? Auch diese Frage hat Cantor gelöst, indem er diesmal zeigte, dass es nicht geht.
Stellen wir uns vor (so sein Argument), wir hätten alle Zahlen irgendwie geordnet. Eine solche Ordnung könnte etwa so aussehen (und stören Sie sich erst mal nicht an den fettgedruckten Ziffern):
1: 0,10110101001…
2: 0,01010010110…
3: 0,00001000010…
4: 0,11010000101…
5: 0,10001010001…
…
Jetzt konstruiert Cantor eine neue Zahl, indem er von der ersten Zahl die erste Ziffer nimmt, von der zweiten Zahl die zweite Ziffer, usw. (im Beispiel: fett gedruckt) und die Zahlen in ihr Gegenteil verkehrt. Daraus erschafft er eine neue Zahl, die in unserem Beispiel so aussieht: 0,00100…
Es gibt viele Zahlen mit einer 0 an erster Stelle, einer 1 an dritter Stelle, usw., aber nicht in dieser Kombination. Also stimmt unsere Aussage nicht, wir hätten alle Zahlen untereinander geschrieben. Also ist c größer als aleph-0 , zumindest um eine Zahl. Weil wir auf diese Weise aber viele Zahlen erzeugen können, kommen unendlich viele neue Zahlen dazu.
Das Argument überzeugte Kritiker wie Poincaré in keiner Weise. Eine Zahl mehr, mühsam konstruiert – was soll’s? Der Rest der Mathematiker aber akzeptierte Cantors Argument und wandte es auch in anderen Situationen an.
Mengen, deren Mächtigkeit gleich c ist, bezeichnet man als überabzählbar. c ist also größer als aleph-0 , aber um wieviel? Diese Frage treibt die Mathematiker auch heute noch um, und die meisten meinen, c wäre sehr viel größer als aleph-0 . Aber was heißt schon „sehr viel“ im Bereich des Unendlichen?