
Das schematische Operieren mit Figuren ist jedem geläufig. Zum Beispiel werden beim Bau einer Mauer die Ziegelsteine nach einem Schema aufeinandergelegt. Beim Stricken werden die Maschen schematisch hergestellt und verknüpft.
Paul Lorenzen, Vertreter einer konstruktiven Mathematik
In der Sciencefiction-Erzählung „Das Gewölbe des Ungeheuers“ von A. E. van Vogt muss der Held, „der beste Mathematiker der Erde“, die größte Primzahl finden, um das Ungeheuer aus seinem Gewölbe befreien zu können. Natürlich weiß van Vogts Held das Gleiche wie wir alle: Es gibt keine größte Primzahl. Also muss diese Zahl unendlich sein. (Frage nebenbei: Ist ω eine Primzahl? Oder ungerade? Oder gerade?)
Um das Primzahlenschloss knacken zu können, muss seine Energie um 1 verringert werden. In unsere Sprache übersetzt: Wir müssen die Zahl ω-1 konstruieren. Und die gibt es bekanntlich nicht.
Oder doch?
1970 dachte sich der Mathematiker James Horton Conway (1937 – ) ein Computerspiel aus, das sich virusartig über alle Computer verbreitet: das „Game of Life“, das Lebensspiel. Mit drei sehr einfachen Regeln ordneten sich chaotisch verteilte Zellen zu überraschend symmetrischen und harmonischen Mustern. Zur gleichen Zeit machte sich Conway Gedanken über einen universalen Konstruktor – und heraus kamen die surrealen Zahlen. Sie werden konstruiert wie Cantors Ordinalzahlen (aber auf andere Weise), doch sind sie reichhaltiger als alles, was sich Mathematiker bisher ausdachten. Nicht nur die reellen Zahlen sind in ihnen enthalten, auch die hyperreellen Zahlen (die „Infinitesimale“ der Analysis) und vieles mehr. Schauen wir uns Conways geniale Konstruktionsmethode etwas näher an!
Ausgangspunkt zur Konstruktion von Zahlen sind nicht unendliche Summen oder Folgen wie bei Cauchy und Cantor, sondern sogenannte Intervallschachtelungen¸ die sich Cantors Zeitgenosse Richard Dedekind (1831 – 1916) ausgedacht hat. Eine Zahl steckt zwischen zwei Zahlen, und die Grenzpunkte dieses Intervalls rücken immer näher aneinander, bis sie (nach unendlich vielen Schritten) die gesuchte Zahl eingeschlossen haben. Auf diese Weise bestimmte Archimedes vor zwei Jahrtausenden den Wert von pi, indem er einen Kreis zwischen regelmäßigen Vielecken „schachtelte“ (solche Vielecke dem Kreis um- und einschrieb).
Conway verwendet also zur Definition zwei Mengen, eine linke und eine rechte, durch den senkrechten Strich (|) voneinander getrennt. Manchmal ist auch nur eine Menge da. Die gesuchte Zahl ist dann die nächste einfachste Zahl vor oder nach einer Zahl oder dazwischen. Das sieht dann so aus (die geschweiften Klammern sind Mengenklammern):
{0|} = 1, {|0} = -1, {0|1} = ½, {0|2} = 1 oder 1½
Daraus folgt aber auch, dass nur Vielfache von ½ möglich sind – wir kommen nie auf 1/3 ! Um also andere Bruchzahlen zu erhalten, muss Conway unendliche Schachtelungen vornehmen, wobei die bekannte Formel hilft:
1 + x² + x³ + … = 1/(1-x)
Interessant sind natürlich Zahlen, die ins Unendliche führen. So gilt natürlich
{0, 1, 2, …|} = ω und {0, 1, 2, …,ω|} = ω+1
Aber weil Conways Definitionen zeitlich gestaffelt sind – manche Zahlen können erst dann erschaffen werden, wenn andere vorher erschaffen wurden – sind auch gänzlich neue und überraschende Zahlen möglich. Angenommen, ω ist schon erzeugt. Dann hat auch diese Definition Sinn: {0, 1, 2, …|ω} = ω-1
Das Ungeheuer kann aus seinem Gefängnis befreit werden!
Und weiter:
{0, 1, 2, …|ω, ω-1, ω-2, … } = ω/2. Man trifft sich sozusagen auf halber Strecke. Das sieht grafisch so aus:
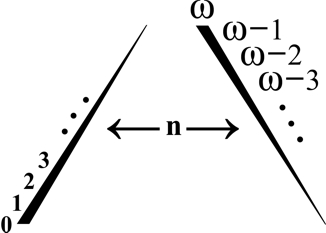
Diese Zahl kann man symbolisch so darstellen: ({n}│{ω-n}). Die beiden Reihen treffen sich bei n, wenn gilt:
n = ω-n, oder n= ω/2
Noch interessanter ist folgende Reihe:
(1,2,3,…│ω/1,ω/2,ω/3,…), oder symbolisch: ({n}│{ω/n})
Auflösung dieser Gleichung liefert n= ω/n, oder n = √ω. Man kann aus unendlich auch die Wurzel ziehen!
Statt ins unendlich Große können wir auch ins unendlich Kleine marschieren:
{0|1, 1/2, 1/4, 1/8, …} = 1/ω, auch als ι (iota) bezeichnet. Das ist eine Zahl zwischen 0 und der kleinsten Zahl >0, passenderweise als Reziprokwert von ω bezeichnet. Wenn es diese Zahl gibt, kann man natürlich weiter machen:
{1/ω|1, 1/2, 1/4, 1/8, …} = (1/ω)/2 = 1/2ω, und auch die Wurzel ziehen:
√ι = (ι, 2ι, 3ι, …│1, 1/2,1/3,…)
Wir sind also schon im Bereich der hyperreellen Zahlen, d.h., wir definieren Infinitesimale. Conway fand auch exakte (aber komplizierte) Definitionen für die arithmetischen Grundrechenarten. Nur mit dem Integrieren gibt’s Probleme, weil einfach zu viele Zahlen vorhanden sind. Und gerade das Integrieren ist des Physikers täglich Brot!
Obwohl Conway mit seinen Zahlen Bereiche erfasste, die anderen verschlossen blieben, musste auch er Grenzen anerkennen, die er Lücken nannte. Conway benannte zwei solcher Lücken (die weder Zahlen noch Mengen noch Klassen noch sonst irgendein sinnvoller Begriff sind, sondern schlichtweg „verbotene Bereiche“):
(1) Die „Lücke“ (eigentlich: die nebelhafte Leere) am Ende der Zahlengeraden, also im Bereich der größten Zahl(en). Wir haben die größte Zahl (die es nicht geben kann) früher mit Ω bezeichnet, und das tut auch Conway.
(2) Die Lücke zwischen der größten ganzen Zahl <ω und der größten reellen Zahl <ω. Conway wählte für diesen Nebelbereich ein bekanntes Symbol: die liegende Acht (∞). Die Zahl liegt zwischen ω-1 und ω, kann aber durch keine Intervallschachtelung erfasst werden.
Jetzt können auch noch die Reziprokwerte definiert werden:
(1a) ist die Lücke zwischen allen denkbaren (kleinen) Zahlen und 1/Ω.
(2a) ist die Lücke zwischen der kleinsten hyperreellen (infinitesimalen) Zahl und 1/∞.
Unanschaulich? Das finden wir auch, drum haben wir versucht, das Ganze darzustellen. Das sieht dann (sicher nicht ganz zutreffend) so aus:

Lücken im unendlich Großen
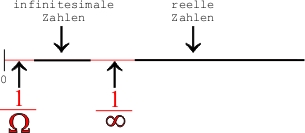
Lücken im unendlich Kleinen
Mit seinen Definitionen gelang Conway eine geradezu magische Formel, welche die drei von ihm definierten Unendlichkeiten in einer Beziehung zusammenfasst:
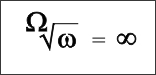
Warum sind seine Zahlen nicht bekannter, warum fungiert seine Formel nicht unter den „zehn schönsten Formeln“? Conways spielerischer Geist passte wohl nicht zur offiziellen Mathematik. Darum beschäftigen sich die Mathematiker immer noch mit unendlich großen (und ziemlich sinnlosen) Kardinalzahlen, statt die hübschen konstruktiven Spiele des originellen Mathematikers weiter auszubauen.
Antwort auf die Frage: Es hängt davon ab, wie wir zu ω gelangen. Beispiele:
1,2,3 … ω: ω ist unbestimmt
1,3,5,… ω: ω ist ungerade
2,4,6,… ω: ω ist gerade
2,3,5,7,11,13,17,… ω: ω ist eine Primzahl
Die Abbildung rechts oben symbolisiert den Aufstieg der surrealen Zahlen vom Endlichen ins absolut Unendliche, das hier sogar explizit in die Konstruktion einbezogen wird.