
Das Unendliche ist dort, wo der Unsinn vernünftig wird.
Carl Friedrich von Weizsäcker
Jetzt wollen wir den Weg weiter gehen, bis zu einer Zahl, die einen kleinen Endpunkt unserer Reise ins absolut Unendliche darstellt. Dazu stellen wir uns Laufbänder vor, die von außen nach innen immer schneller werden.
Auf dem ersten (äußersten) Laufband addieren wir:
ω, ω+1, ω+2, … ω+ω = ω x 2
Auf dem nächsten, schon etwas schnelleren Laufband multiplizieren wir:
ω x 2, ω x 3, … ω x ω = ω²
Auf dem dritten Laufband müssen wir aufpassen, nicht herunter zu fallen, denn dort exponentieren wir:
ω², ω³, ω^4, … ω^ω
Jetzt sind wir ganz schön weit, ohne uns sonderlich angestrengt zu haben. Auf dem innersten, dem schnellsten Laufband, wagen wir die letzten, wirklich großen Sprünge:
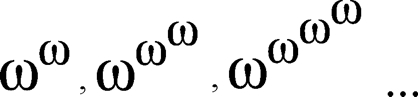
Der allerletzte Sprung besteht aus unendlich vielen Exponenten ω zur Basis ω. Diese Zahl nannte Cantor ε0 („epsilon-null“), und dort hörte seine Reise ins Unendliche vorläufig auf. Diese Zahl sieht also so aus::

Der letzte Ausdruck bedeutet: ω, ω-mal tetriert.
Eine gewaltige Zahl, mit der bemerkenswerten Eigenschaft, dass
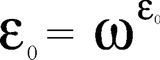
denn ein ω mehr oder weniger macht hier nichts aus! Natürlich können wir, nach einer geeigneten Verschnaufpause, weiter den Himmel des Unendlichen erklimmen und z.B. ε1 definieren als
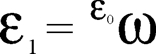
also ω, ε0-mal tetriert. Unvorstellbar, im Unendlichen aber immer noch eine Erdnuss (neudeutsch: peanut). Und so geht es mit den Indizes weiter, bis zu εω und so weiter. Jetzt kann man die unendliche Folge auch nach unten fortsetzen, d.h. eine ε-Zahl mit unendlich vielen Indizes finden. Die sieht dann so aus:
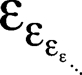
… und wie groß die ist, kann sich niemand vorstellen! Jedenfalls gilt auch für diese gigantische Zahl eine Gleichung, nämlich
εα = α
Cantor nannte seine unendlich großen Zahlen nicht infinit (= nicht-endlich), sondern transfinit (= jenseits des Endlichen). Dieses Wort hat Anklänge an „transzendent“, also jenseits unserer Erfahrung, mit anderen Worten: spirituell, religiös. Und da sich Cantor viel mit theologischen Spekulationen beschäftigt hat, passt auch diese Bezeichnung recht gut zu seinen Schöpfungen.
Brauchen wir solche Zahlen irgendwo? Im Prinzip nein (auch nicht in der Mathematik); allerdings hat ε0 eine gewisse Bedeutung. Der deutsche Mathematiker Gerhard Gentzen (1909 – 1945) hat bewiesen, dass die Arithmetik widerspruchsfrei ist. Dabei benutzte er unendlich lange Ausdrücke; die Wortlänge würde allerdings, so versicherte er, niemals die Zahl ε0 überschreiten. Ob so etwas überhaupt zulässig wäre, darüber streiten die Gelehrten heute noch.
Und das war’s! Die Reise mit nur zwei Operationen, dem Nachfolger und dem Limes, geht damit zu Ende. Cantor verfolgte diese Zahlenfolge nicht weiter, sondern wandte sich anderen Zahlen zu, den Kardinalzahlen. Mit denen konnte man viel fantastischere Dinge machen, weil bei ihnen nicht mehr gezählt, sondern definiert wurde. Mathematik ist Freiheit sagte Cantor einmal, und diese Freiheit trieb die erstaunlichsten Blüten.
Somit beginnen wir mit dem nächsten Kapitel etwas völlig Neues. Die ganze Fähigkeit des abstrakten und unbeschränkten Denkens wird uns mit den Kardinalzahlen zu atemberaubenden Erkenntnissen führen. Nehmen wir also Abschied von den einfachen Zählzahlen, deren korrekte Bezeichnung Ordinalzahlen lautet und deren Aufgabe bloß darin besteht, irgendwelche Elemente durchzunummerieren. Sie dienen dem Auf- und Weiterzählen, man kann sie in eine Ordnung bringen (daher der Name), es ist also immer möglich, von zwei Ordinalzahlen zu sagen, welche die größere und welche die kleinere ist. Doch im Meer der Unendlichkeit sind sie nur ein paar Kräuselwellen im flachen Sandstrand.
Das Cantorsche Verfahren zur Erreichung einer hohen transfiniten Zahl ist uralt. Bereits Archimedes (287 – 212 v. Chr.) verwendete es in seiner berühmten „Sandrechnung“. Ausgangspunkt war die damals höchste bekannte und darstellbare Zahl, eine „Myriade“, lächerliche 10.000 (= 10^4). Die verwendete er doppelt, womit sich ergab: eine Myriad-Myriade = MM = 10^8. So ging er in Stufen und Perioden vor:
MM, 2MM, … , MMxMM = MM²
… MM³
…
… MM^MM
… und schließlich MM zu MM tetriert (MM hoch MM hoch MM hoch …, insgesamt MM-mal). Archimedes ging aber nur bis MM zu 3 tetriert und kam so zuletzt auf die Zahl von 10^63 Sandkörnern, was, umgerechnet auf Elementarteilchen, in etwa dem entspricht, was Astronomen nach der Urknallhypothese von der Größe und Masse des Weltalls annehmen.
Die Abbildung rechts oben stammt aus einem Artikel über das Unendliche, der im P.M.-Magazin 2007 erschien und vom Verfasser dieses Buchs sowie vom P.M.-Chefredaktör Thomas Vasek geschrieben wurde. Das Bild zeigt den Aufstieg zu immer höheren Ordinalzahlen. In der Ferne glänzt das stets unerreichbare Absolute. Wir werden das Symbol des senkrechten Aufstiegs noch ein paar Mal verwenden!