Alles, worauf ein Mensch sich ernstlich einläßt, ist ein Unendliches.
Johann Wolfgang von Goethe
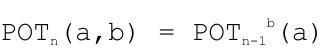
Wir sind immer noch im Endlichen, aber jetzt basteln wir uns einige wirklich große Zahlen zusammen. Doch erst müssen wir die üblichen arithmetischen Operationen definieren, d.h. auf schon Bekanntes zurückführen. Schauen wir uns die Sache an ein paar Beispielen ein wenig näher an! Z.B. 5 + 2. Das sieht in unserer symbolischen Schreibweise so aus:
(1) IIIII II –> IIIIIII
Und umgekehrt? 2 + 5 sieht so aus:
(2) II IIIII –> IIIIIII
Das Resultat ist das Gleiche (nämlich 7), aber die Vorgangsweise ganz unterschiedlich. Im ersten Fall haben wir 2-mal den Nachfolger von 5 bestimmt, im zweiten Fall 5-mal den Nachfolger von 2. Da man die beiden Zahlen vertauschen kann, und da vertauschen im lateinischen „commutare“ heißt, nennt man deswegen die Addition kommutativ. Nicht jede mathematische Operation muss kommutativ sein, und im Unendlichen schon gar nicht!
Jedenfalls können wir die Addition auf die Nachfolger-Operation zurückführen, indem wir schreiben:
ADD(a,b) = NFL^b(a)
(Die Addition zweier Zahlen a und b besteht in einer b-maligen Anwendung der Nachfolge-Operation auf a.)
Das Gleiche wird uns wohl auch mit der Multiplikation gelingen. Wir wollen sie auf die Addition zurückführen und schauen uns die Vorgangsweise wieder an einem Beispiel an. 2 x 5 sieht in unserer Schreibweise so aus:
(1) II II II II II –> IIIIIIIIII
Umgekehrt: 5 x 2 sieht so aus:
(2) IIIII IIIII –> IIIIIIIIII
Auch hier sehen wir, dass sich bei Vertauschen der Faktoren ganz unterschiedliche Muster entstehen. Bei 2 x 5 haben wir 5-mal das Muster „II“ nebeneinander gestellt; bei 5 x 2 haben wir 2-mal das Muster „IIIII“ nebeneinander gestellt. Das Endresultat ist das Gleiche – im Endlichen.
Also können wir definieren:
MUL(a,b) = ADD^b(a)
Die Multiplikation zweier Zahlen a und b besteht in einer b-maligen Anwendung der Addition auf a.)
In der Schule haben wir gelernt, dass die Exponentiation (Potenzbildung) nichts anderes ist als eine wiederholte Multiplikation:
2^5 („2 hoch 5“) = 2 x 2 x 2 x 2 x 2 (= 32), oder:
EXP(a,b) = MUL^b(a)
(Die Exponentiation von a^b besteht in einer b-maligen Anwendung der Multiplikation auf a.)
Jetzt kommen typisch mathematische Überlegungen. Nachdem die Rückführungsgesetze alle gleich aussehen, könnten wir doch diese drei Gesetze zu einem einzigen zusammenfassen. Dazu brauchen wir einen neuen Namen für die verallgemeinerte arithmetische Operation. Nennen wir das ganze POTENZ, abgekürzt POT. Ferner brauchen wir jetzt noch einen Index, eine Zahl, die uns angibt, um welche Operation es sich handelt. Ein Index wird normalerweise tiefgesetzt; was wir hier nicht können; und in kleinerer Schrift geschrieben, was wir hier auch darstellen:
POT0 = Nachfolger
POT1 = Addition
POT2 = Multiplikation
POT3 = Exponentiation
und allgemein gilt dann also:
POTn (a,b) = POT(n-1)^b(a)
(korrekte Schreibweise: siehe Bild rechts oben)
Wozu der Aufwand? werden manche fragen. Doch jetzt, nach diesen umständlichen Vorbereitungen, zeigt sich die ganze Stärke mathematischer Denkweise und Symbolik. Denn jetzt können wir fragen: Was bedeutet eigentlich POT4 oder POT5 oder … ?
POT4(a,b) bedeutet die b-malige Anwendung von POT3, also der Exponentiation. D.h.,
POT4(2,5) = 2^2^2^2^2, eine Zahl, die man kaum ausrechnen, aber immerhin noch hinschreiben kann. Diese Rechenoperation hat auch den Namen „Tetrierung“ (von griechisch „tetra“ = vier, die Nummer des Index), und man schreibt sie manchmal in dieser Form:
ba („a, b-mal tetriert“)
Dagegen können wir POT5 nicht mehr hinschreiben und schon gar nicht ausrechnen.
Der deutsche Mathematiker Wilhelm Ackermann (1896-1962) hat sich eine Funktion ausgedacht, in der er diese Stufenfolge der arithmetischen Operationen rekursiv zusammengefasst. Wir haben gleich das entsprechende BASIC-Programm hingeschrieben. Aber Vorsicht beim Ausprobieren! Bis m=3 geht alles gut, doch ab m=4 bricht der Computer zusammen.
FUNCTION acker (m, n)
IF n < 0 THEN
EXIT FUNCTION
ELSEIF m = 0 THEN
acker = n + 1
ELSEIF n = 0 THEN acker = acker(m – 1, 1)
ELSE acker = acker(m – 1, acker(m, n – 1))
END IF
END FUNCTION
Der Mengentheoretiker Harvey M. Friedman von der Ohio State University hat mit Hilfe der Ackermann-Funktion eine eigene Funktion definiert – nennen wir sie FRIED(n) – , die derart schnell wächst, dass ab n=3 ihr Wert nicht mehr errechnet werden kann. Friedman fand heraus: FRIED(1)=3, FRIED(2)=11, und das war’s. FRIED(3) ist, nach Computer-Berechnungen, größer als acker(7198,158386), eine unvorstellbare Zahl. FRIED(4) kann man mühsam noch irgendwie hinschreiben. Dazu definiert man A(n) = acker(n,n) (Diagonalisierung der Ackermann-Funktion). Dann ist FRIED(4) größer als AA…A(1), wobei A insgesamt so oft vorkommt, wie der Wert von A(187196) ergibt. Friedman nennt seine Zahlen „enorm“, eine milde Untertreibung!