
Das Studium des Unendlichen ist weit mehr als ein trockenes akademisches Spiel. Die geistige Erforschung des absolut Unendlichen ist eine Form der Seelensuche nach Gott. Ob das Ziel je erreicht wird oder nicht, das Bewusstsein dieses Wegs bringt Erleuchtung.
Rudy Rucker: Infinity and the Mind
Es ist leicht zu zeigen, dass es „gleich viele“ ganze Zahlen, gerade Zahlen, Quadratzahlen, Primzahlen, usw. gibt: Wir bilden Paare zwischen den ganzen Zahlen (unsere Vergleichsmenge) und den Zahlen, die wir zu einer Menge zusammenfassen. Beispiel Primzahlen:
| M1 | Vergleichsmenge | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
| M2 | zu messende Menge | 2 | 3 | 5 | 7 | 11 | 13 | 17 | … |
Die drei Punkte zeigen, dass beide Mengen ins Unendliche fortgesetzt werden können und deswegen also gleich viele Elemente enthalten, auch wenn die untere Menge eine echte Teilmenge der oberen Menge darstellt. Also gilt beispielsweise:
Mächtigkeit(Menge der Primzahlen) = aleph-0, und das gilt für alle Mengen natürlicher Zahlen, die unendlich viel davon enthalten.
Aber wie viele Bruchzahlen gibt es? Die alten Griechen nannten sie „rationale Zahlen“, weil sie Zahlen nur als Brüche darstellen konnten und die unendliche Dezimalbruchentwicklung nicht kannten. Bruchzahlen gibt es unendlich viele allein zwischen 0 und 1, und dann erst recht zwischen 0 und unendlich. Bruchzahlen liegen „dicht“, was bedeutet, dass man zu beliebig benachbarten Bruchzahlen immer noch eine (und damit unendlich viele) findet.
Ihre Anzahl, also, korrekt: die Mächtigkeit der Menge der Bruchzahlen zwischen 0 und 1, sollte demgemäß größer sein als die der ganzen Zahlen. Ist sie aber nicht, wie Cantor zur eigenen Überraschung feststellte. Denn er konnte die Brüche eindeutig den ganzen Zahlen zuordnen – und damit ist ihre Mächtigkeit gleich der Mächtigkeit der ganzen Zahlen, also gleich aleph-0. Wie hat er das gemacht? Etwa so:
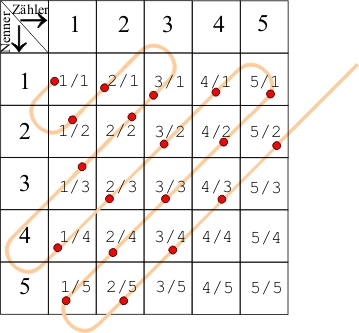
Cantor bastelte sich ein zweidimensionales Schema, eine Matrix, und fädelte die Brüche auf wie in den Frühzeiten der Datenverarbeitung die Kernspeicher aufgebaut waren: Ein Faden (der Abzählfaden) durchläuft alle Felder der Matrix, mithin alle Bruchzahlen. Stören Sie sich nicht daran, dass viele Zahlen doppelt vorkommen oder gar nicht erfasst werden sollen. Die oberste Reihe ist zum Großteil überflüssig, weil sie nur ganze Zahlen betrifft, und wir brauchen davon aber nur die 1 (wir betrachten ja nur die Bruchzahlen zwischen 0 und 1). In der Hauptdiagonale steht außerdem immer die gleiche Zahl, nämlich 1. Und viele Brüche wiederholen sich, beispielsweise 2/4. Das hatten wir schon als 1/2. Egal, was wir brauchen, haben wir erreicht: Jede Bruchzahl kommt in dieser Abzählung mindestens einmal vor. Und weil wir alles abzählen können, heißt eine solche Menge abzählbar. Die Mächtigkeit jeder abzählbaren Menge ist immer gleich aleph-0.
Erstaunlich: Diese dichte Menge kann man nicht nur abzählen, man kann ihre Mitglieder auch in eine ganz bestimmte Reihenfolge bringen. Wir können zwar nicht sagen, welches die erste Bruchzahl rechts von der 0 ist (also die kleinste Bruchzahl > 0), wohl aber können wir sagen, welches die erste Bruchzahl nach der Cantorschen Aufzählung ist, nämlich 1.
Noch erstaunlicher: Cantor fand eine einfache Formel („pi“), mit deren Hilfe jedem Bruch (auch solchen > 1) eine eindeutige ganze Zahl zugeordnet werden kann:
pi(a,b) = (a+b)(a+b+1)/2+a
Neben einer dichten, aber abzählbaren Menge konstruierte Cantor auch das genaue Gegenteil: eine undichte („magere“), aber überabzählbare Menge, den nach ihm benannten Cantor-Staub. Die Konstruktion dieses paradoxen Gebildes ist verbal ganz einfach: Man nehme aus der Einheitsgeraden (die 0 mit 1 verbindet) das mittlere Drittel heraus. Mit den jetzt erschaffenen zwei Geraden tut man das Gleiche – ad infinitum. Das sieht dann so aus:

Das Gebilde zerfasert im Limit zu einer Menge isolierter Punkte, und sogar seine Länge geht gegen 0, aber die Anzahl der Punkte bleibt immer gleich: Sie ist gleich der Mächtigkeit des Kontinuums. So grotesk und konstruiert das Ganze aussieht, Wissenschaftler fanden sogar Anwendungen dafür: Die Saturnringe ähneln ihm, ebenso die Spektren mancher organischer Moleküle (siehe Bild rechts oben: Was im Vordergrund wie ein Vorhang aussieht, ist eine besondere Darstellung des Cantorstaubs: Es wird nach unten zu immer dünner, bis nur noch isolierte Einzelpunkte übrig bleiben – aber überabzählbar viele!).
So paradoxe Resultate kommen in der Theorie der transfiniten Zahlen ständig vor. Ein Hauptgrund dafür liegt darin, dass dabei versucht wird, geometrische Gebilde (eine Linie) durch Zahlen zu beschreiben. Jeder denkbaren Zahl soll ein Punkt entsprechen, was nicht weiter schwierig ist. Jedenfalls dann nicht, wenn es sich um eine Bruchzahl (eine „rationale“ Zahl) handelt, denn die kann man einfach mit Zirkel und Lineal in eine Strecke verwandeln. Mit irrationalen oder transzendenten Zahlen wird das schon schwieriger. Wenn aber auch noch jedem Punkt eine Zahl entsprechen soll, dann ist das praktisch unmöglich: Woher weiß ich denn, wie der Punkt definiert ist? Das geht im Prinzip nur durch den Schnitt zweier Geraden, doch so etwas kommt in der Mengenlehre nicht vor.