In der Mathematik ist die Erkenntnis eines Problems schwieriger als dessen Lösung.
Georg Cantor
Im Mittelalter beschäftigten sich gelehrte Denker viel mit dem Unendlichen, meist im Zusammenhang mit Gott. Aber auch rein mathematische Überlegungen führten zu höchst modernen Erkenntnissen. Bereits Roger Bacon (1210-1292) stellte eine Beziehung zwischen zwei ungleichen Mengen her und erkannte, dass die Mengen gleich umfangreich („gleich groß“) sind. Er verband einfach jeden Punkt der Quadratseite mit dem entsprechenden Punkt der zugehörigen Diagonale. Es sind nun gleich viele Punkte (natürlich unendlich viele), und doch sind die Seiten verschieden lang. Bacon folgerte daraus, dass das Unendliche im Bereich der Geometrie nichts zu suchen hatte.
Der Philosoph Albert von Sachsen (1316/1325 – 1390) formuliert diese Erkenntnis erstaunlich modern: Wenn zwei Mengen sich so verhalten, dass jeder Einheit der einen eine Einheit der anderen entspricht, dann ist die eine weder größer noch kleiner als die andere.
Also mit anderen Worten: Dann sind die Mengen einander gleich, auch wenn sie sehr unterschiedlich sind. Galileo Galilei (1564 – 1642) griff den Gedanken auf und ordnete die Menge der ganzen Zahlen der Menge der Quadratzahlen zu:
| 1 | 2 | 3 | 4 | 5 | … |
| ! | ! | ! | ! | ! | |
| 1 | 4 | 9 | 16 | 25 | … |
Nachdem beide Reihen bis ins Unendliche fortgesetzt werden können, folgerte Galilei, dass die beiden Mengen gleich groß sind, obwohl die untere Menge eindeutig wesentlich weniger Elemente enthält als die obere (sie ist eine echte Untermenge der oberen). Woraus Galilei folgerte: Begriffe wie „kleiner“, „gleich“, „groß“ haben im Unendlichen keine Bedeutung, und deswegen solle man sich damit nicht beschäftigen.
Genau andersherum dachte Georg Cantor (1845-1918). Für ihn war diese Zuordnungsmethode Ausgangspunkt seiner Lehre von den transfiniten Zahlen (Zahlen jenseits des Endlichen, über das Endliche hinausführend). Er machte daraus ein großartiges Werkzeug, das in ungeahnte geistige Höhen führte. Wir sehen: Die gleichen Fakten können ganz unterschiedlich aufgefasst werden. Der eine resigniert, der andere triumphiert – fast wie im richtigen Leben.
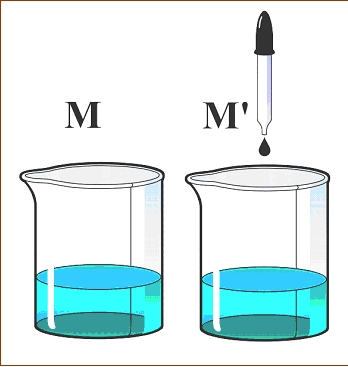
Dabei ist es gar nicht so schwierig sich vorzustellen, dass zwei unterschiedliche Mengen gleich groß sind („gleich mächtig“, wie man sagt). Stellen wir uns vor, wir hätten eine „Menge“ Wasser (M), die beim Abwiegen genau einen Liter wiegt. Jetzt geben wir einen Tropfen Wasser dazu und erhalten dadurch die Menge M‘. Es ist klar, dass M‘ > M, und dennoch ergeben noch so genaue Messungen, dass das Gewicht (die Größe) der Menge M gleich dem der Menge M‘ ist. Also ist es auch im Endlichen möglich, dass eine echte Untermenge (hier: M) genauso mächtig ist wie die Menge selbst (hier: M‘). (siehe Bild rechts oben)