Damals studierte er Mathematik; aber später ist er ein Dichter geworden. Zur Mathematiker hatte er nicht genug Phantasie.
David Hilbert
In Büchern über das aktual Unendliche wird oft das Beispiel von Hilberts Hotel genommen, um zu zeigen, was im Unendlichen alles möglich ist. David Hilbert (1862 – 1943) war ein glühender Verehrer Cantors und dachte sich folgenden Vorgang zur Illustrierung von Cantors Ideen aus: Sein Hotel besteht aus ω Zimmern, von denen jedes nur eine Person fasst. (Denken Sie an japanische Hotels und ihre Schlafkojen.)
Eines Tages war das Hotel voll, bis auf den letzten Platz. Ein später Besucher begehrte dennoch Einlass, und der wurde ihm auch gewährt. Alle Besucher rückten um einen Platz nach rechts, also dorthin, wo sich das Hotel ins Unendliche erstreckt. So wurde das erste Zimmer frei, und unser später Gast konnte sich zur wohlverdienten Ruhe niederlegen.
Bloß, wie ist das wirklich gegangen? Etwa so:
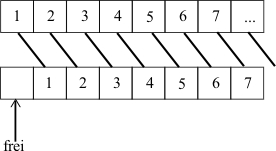
Alle Zimmerinsassen rückten um einen Platz nach rechts, aber gleichzeitig, weil in einem Zimmer nicht mehr als eine Person Platz hat. Aber wie soll dieses „gleichzeitig“ vor sich gehen? Einer muss den Befehl geben, doch der muss sich unendlich schnell ausbreiten, was nicht möglich ist, nicht mal in der Mathematik. Also haben sich die Mathematiker die Erlaubnis für einen unendlich schnellen, gleichzeitigen Wechsel selbst gegeben. Das Ganze nannten sie Auswahlaxiom (zuerst formuliert von Ernst Zermelo), weil es jeden Mathematiker befähigen soll, aus unendlich vielen Mengen gleichzeitig mindestens ein Element auszuwählen.
Was dadurch möglich wurde, brachte die Mathematik ziemlich durcheinander und stieß auch vielen Mathematikern sauer auf. Denn durch das Verschieben haben wir ein Element dazu gewonnen, allein durch Umschichten, was ja nicht gerade eine kreative Tätigkeit ist. Wenn wir es geschickt anstellen, dann können wir links auch unendlich viele Gäste zusätzlich unterbringen – die Menge hätte sich also verdoppelt.
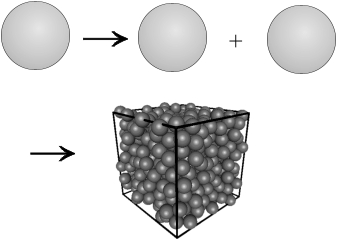
Die beiden polnischen Mathematiker Stefan Banach (1892 – 1945) und Alfred Tarski (1902 – 1983) konstruierten daraus ein kurioses Paradoxon, das nach ihnen benannt wurde. Sie zerlegten eine Kugel in fünf Teile. Einer davon ist nur ein Punkt (der Mittelpunkt), der Rest vier gleich große Mengen, also Viertelkugeln. Durch geschicktes Drehen werden immer mehr Punkte hinzugefügt, sodass zwei der Viertelkugeln zu Dreiviertelkugeln anwachsen. Das ergibt dann als Maß der Kugel: 2 x ¾ + 2 x ¼ = 8/4 = 2. Die Kugel hat sich verdoppelt, aus eins mach zwei, wir waren dabei.
Banach und Tarskis magische Kugel: Durch einfache Drehungen verdoppelt sie sich erst, bis man sie beliebig vervielfachen kann – Mathematik oder Magie?
Angeblich haben sich Banach und Tarski die magische Kugel ausgedacht, um den Unsinn des Auswahlaxioms zu demonstrieren. Sollte das wirklich ihre Absicht gewesen sein, sie ist ihnen gründlich misslungen. Die Mathematiker – jedenfalls die Anhänger Cantors – sind stolz auf diese Erkenntnis, auch wenn aus ihr folgt, dass es Mengen gibt, die man nicht messen kann. Und mit denen ist natürlich alles Mögliche möglich, doch vieles davon bleibt unmöglich.