Das Unendliche hat wie keine andere Frage von jeher so tief das Gemüt der Menschen bewegt. Das Unendliche hat wie kaum eine andere Idee auf den Verstand so anregend gewirkt. Das Unendliche ist aber auch wie kein anderer Begriff der Aufklärung bedürftig.
David Hilbert

Aber jetzt wird’s Zeit: Nach diesen Vorbereitungen wagen wir den Sprung ins Unendliche. Doch wie bewerkstelligen wird das? Mit den bisher gefundenen Operationen bleiben wir immer im Endlichen. Um ins Unendliche zu gelangen, brauchen wir schlicht und einfach eine neue Operation. Wir nennen sie LIMES, abgekürzt LIM, und manche Leser kennen den Ausdruck vielleicht noch aus dem Mathe-Unterricht, wo er bei der Berechnung von unendlichen Reihen verwendet wird. (Oder vom Geschichtsunterricht, wo die Römer so was hatten. Aber das ist eine andere Geschichte.)
Wir haben einen Namen für die Operation, jetzt fehlt uns noch ein Name für das Ergebnis. Georg Cantor, von dem alle diese Ideen stammen, wählte dazu den letzten Buchstaben des griechischen Alphabets, ω („klein-omega“). Also gilt:
LIM(n) –> ω (n = beliebige endliche Zahl),
oder kürzer: 1 2 3 … ω
Die drei Punkte bedeuten also: Wage den Sprung, fürchte dich nicht vor dem Abgrund, lande bei ω. Jetzt brauchen wir noch ein Symbol für ω. Dafür nehmen wir eines, das der Mathematiker und Erfinder des Computer-Spiels LIFE, James Horton Conway, sich ausgedacht hat:
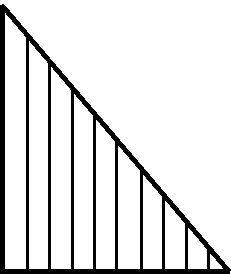
Es soll die Telegrafenmasten symbolisieren, die auf ihrem Weg ins Unendliche immer kleiner werden. Nun gut, jetzt sind wir auf der Ebene „ω“ gelandet; und was weiter? Haben wir den Endpunkt unserer Reise erreicht, oder sind wir nach einer Himmelfahrt auf einer Plattform gelandet, von der aus es weiter geht, in ungeahnte Höhen?
Warum nicht all das anwenden, was wir bisher erarbeitet haben? Wir können doch fragen, ob ω einen Nachfolger hat. Einen Vorgänger hat ω bestimmt nicht, denn „einen Schritt vor unendlich“ gibt es nicht. In dieser Hinsicht gleicht ω der Null. Doch einen Nachfolger hat die erste, die kleinste aller unendlich großen Zahlen, allemal, nämlich
ω‘ = ω + 1
So einfach ist das. Doch wie sieht das Ganze symbolisch aus? Wir verwenden wieder unsere vertrauten Symbole:
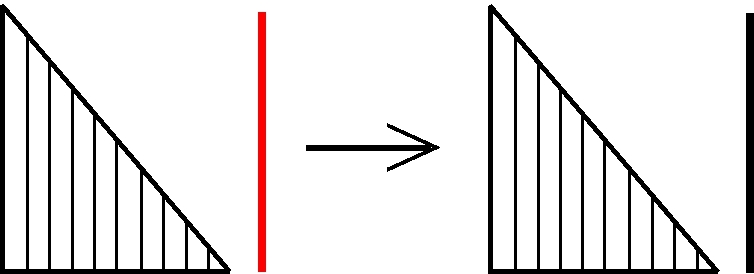
Wir haben also einfach ein Stäbchen rechts angefügt. Aaaaaaber: Wie ist das umgekehrt? Was ergibt 1 + ω? Unsere grafische Darstellung verhilft uns zur Erkenntnis:
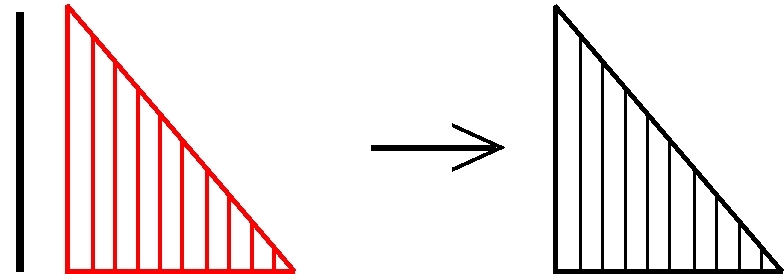
Das Hinzufügen eines Stäbchens auf der linken Seite ändert nichts, weil es im Unendlichen untergeht (siehe auch unser Zwischenspiel über „Hilberts Hotel“). Und das bedeutet:
1 + ω = ω
Das kommutative Gesetz der Addition ist im Unendlichen nicht erfüllt! Da schleicht sich der Verdacht ein, dass es mit der Multiplikation ähnlich sein könnte. In der Tat ergibt ω x 2 das Symbol für ω verdoppelt:
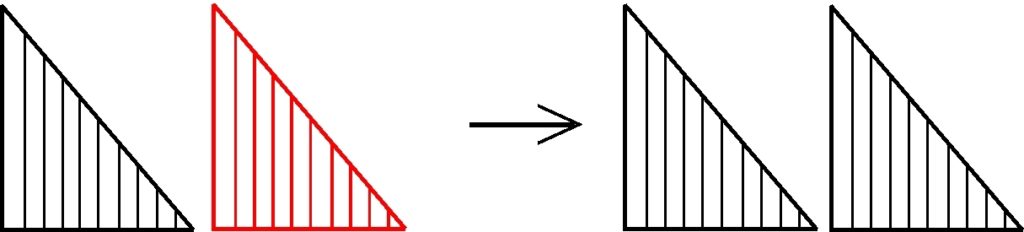
aber 2 x ω ergibt die 2, ω-mal nebeneinander gestellt:
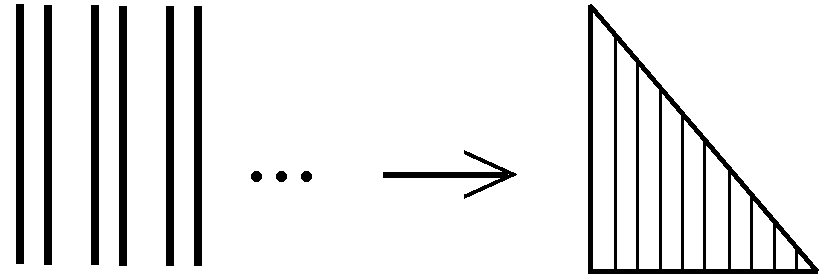
d.h., 2 x ω = ω.
Die Exponentiation ist sowieso schon nicht kommutativ, doch auch hier ergeben sich erst mal überraschende Resultate. Zwar ist ω² tatsächlich gleich ω x ω, aber 2ω = 2x2x2x … = ω. Im Unendlichen ist eben manches anders.
Wie weit ist die 17 von ω entfernt? Unendlich weit. Und die 23? Ist diese Zahl um 6 Einheiten näher an ω? Mitnichten. Jede Zahl, und sei sie noch so groß, ist von ω gleich weit entfernt. Daraus ergeben sich interessante theologische Spekulationen (die uns gestattet sind, weil Cantor Ähnliches getan hat). Identifizieren wir vorläufig ω mit Gott und die endlichen Zahlen mit den Menschen, dann ergibt sich daraus:
(1) Die Menschen sind untereinander verschieden. (17 ist kleiner als 23)
(2) Vor Gott sind alle Menschen gleich (17 und 23 sind von ω gleich weit entfernt).
Ersteres führte zum mittelalterlichen Ständestaat: Ganz unten stehen Bauern und fahrendes Volk, dann kommen Bürger, niedere Adel, Geistliche, zuletzt Papst und Kaiser.
Letzteres führt zur Botschaft der biblischen Propheten: Wenn vor Gott alle Menschen gleich sind, haben sie vor IHM auch die gleichen Rechte. Und da Gott allen Menschen eine unsterbliche Seele gab, ist diese Seele vor Gott gleichwertig, unabhängig von der Stellung des Einzelnen in der Gesellschaft. Daraus ergeben sich so seltsame (und nicht-christlichen Gesellschaften unverständliche) Ideen wie Menschenwürde und Menschenrechte. Und das alles wegen der Eigenschaft von ω!