Mathematik ist die Kunst, verschiedenen Dingen den gleichen Namen zu geben.
Henri Poincaré
Cantor hatte zwei Stufenfolgen des Unendlichen geschaffen: die Potenzmengenbildung (2^x) und die Aleph-Reihe (aleph-0, aleph-1, … ,aleph-ω, …). Die kleinste Zahl der ersten Reihe ist 2^aleph-0 (= c), die der zweiten aleph-1. Es ist ziemlich schwer zu erklären (oder sich gar vorzustellen), worin sich die beiden unterscheiden. Versuchen wir es!
aleph-1 ist die Menge aller abzählbaren Ordinalzahlen, also eine wohlgeordnete Stufenfolge von Ordinalzahlen. Dagegen ist c die Menge aller möglichen Mengen mit abzählbar unendlichen vielen Elementen. Sie ist nicht wohlgeordnet, kann es aber theoretisch werden, was bisher allerdings niemandem gelungen ist.
Umgekehrt: c ist vergleichbar mit einem Klon: Es wird nach Plan gefertigt, (fast) jeder Schritt ist überprüfbar, das Endprodukt steht fertig und für jedermann sichtbar da. aleph-1 hingegen ist wie eine Fabelgestalt, eine Elfe oder ein Kobold: Manche behaupten, es gibt sie, doch die wirkliche Form bleibt der Fantasie überlassen, ebenso die Tatsache, ob aleph-1 existiert oder nicht.
Jetzt wäre es natürlich schön herauszufinden, welche Beziehungen zwischen den Zahlen dieser Reihe bestehen, der Potenzmengenreihe und der aleph-Reihe. Insbesondere meinte Cantor, die ersten Zahlen nach aleph-0 in jeder Reihe wären identisch, also kurz gesagt
2^aleph-0 (= c) = aleph-1
Diese (nicht bewiesene!) Beziehung heißt Kontinuumshypothese. Stimmt sie nicht, dann kann nur gelten 2^aleph-0 > aleph-1, denn aleph-1 ist ja die nächste (also kleinste) Zahl nach aleph-0 und damit sicher nicht größer als 2^aleph-0. Cantor verwendete einen Großteil seiner Zeit und Energie darauf, die Beziehung zu beweisen. Er scheiterte und erlitt einen Nervenzusammenbruch. Kurt Gödel (1906 – 1978) verwandte einen Großteil seiner Zeit und Energie darauf, die Beziehung zu beweisen. Er scheiterte und erlitt einen Nervenzusammenbruch. Nichtsdestotrotz kam Gödel 1938 zu einer erstaunlichen Erkenntnis: Die Kontinuumshypothese kann gar nicht beweisen werden! 1963 beendete der amerikanische Mathematiker Paul Cohen die Debatte ein für allemal, indem er nachwies, dass die Kontinuumshypothese auch nicht widerlegt werden kann. Damit war gezeigt: Sie ist unabhängig von den Axiomen der Mengenlehre; man kann sie akzeptieren (was kaum jemand tut) oder verwerfen (was die meisten Mathematiker machen, indem sie meinen, 2^aleph-0 wäre wesentlich größer als aleph-1).
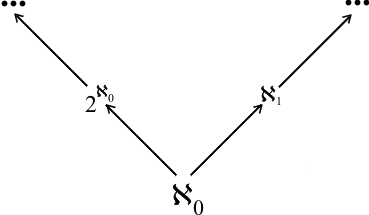
Es sieht also so aus, als hätte Cantor mit seinen beiden Stufenfolgen des Unendlichen zwei voneinander unabhängige Treppen erschaffen, die in völlig unterschiedliche Gefilde führen (siehe Bild rechts oben). Die alephs sind nicht vergleichbar den Potenzmengen, eine erstaunliche Entwicklung. Nun könnte man die Kontinuumshypothese oder ihr Gegenteil als zusätzliches Axiom den bisherigen Axiomen der Mengenlehre hinzufügen, doch das hat bisher niemand getan. Offenbar lieben Mengentheoretiker ihre Freiheit und lassen sich durch ein neues Axiom nicht einengen.