
Das Wesen der Mathematik liegt in ihrer Freiheit.
Georg Cantor
Ein paar Höhepunkte der Stufenfolge der Alephs wollen wir noch zeigen.
Zuvor: Man kann die Kardinalzahlen (die alephs) genauso als Ordinalzahlen einsetzen. Jeder Kardinalzahl entspricht eine Ordinalzahl, aber nicht umgekehrt. aleph-0 entspricht ω, aber ω+1 hat kein aleph als Entsprechung. Es gibt also wesentlich mehr Ordinalzahlen als Kardinalzahlen.
Die Mathematiker haben gezeigt, wie man Ordinalzahlen durch Kardinalzahlen definieren kann. Anstatt von ω nehmen wir auch aleph-0. So können wir die Indizes der alephs so verwenden wie früher die Ordinalzahlen. Die Reihe sieht erst mal so aus:
aleph-0,aleph-1,… aleph-ω = aleph-aleph-0,… aleph-aleph-1 … aleph-aleph-ω
Fortsetzungen ins Unendliche kennen wir ja schon; jetzt wenden wir die Limesbildung auf die Indizes an. Dann erhalten wir eine Zahl, die so aussieht:
aleph-aleph-aleph-aleph-… (siehe Bild rechts oben)
Wieder sträubt sich die Vorstellung: Ein Index, der nach unten ins Unendliche geht. Eine Zahl x, die in einer unendlichen Folge die x-te Zahl ist. Ein Bereich im unendlichen Ozean, wo die Größe der Zahl und ihre Zählung miteinander verschmelzen. Nennen wir diese Zahl θ („theta“). Dann gilt offenbar (was wir durch Einsetzen nachprüfen können):
θ = aleph-θ
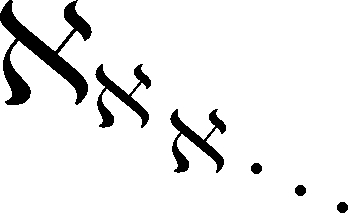
Was bedeutet: Der Index ist genauso groß wie die Zahl selbst! Normalerweise ist die Zahl gigantisch größer als der Index, aber hier ist sie gleich. Diese Zahl hat eine „Fixpunkteigenschaft“ in Bezug auf den Index. Sie ist die größte Zahl, die sich Mathematiker im Bereich der alephs ausgedacht haben – allerdings haben wir diese Konstruktionsform schon bei den Ordinalzahlen, bei ε, kennen gelernt.
Noch weiter geht es nur über seltsame Definitionen. Davon demnächst mehr!